Introduction to Statistics in Finance

Introduction to Statistics in Finance#

Many fields in finance rely on some sort of data analysis

For example fundamental analysis of a business:
- various numbers from the company itself (i.e. from the balance sheet)
- indicators representing the overall market

Results drive decisions, e.g. for an investement

There are many well established techniques and statistics for pricing financial products.

Some techniques more prominent since the dawn of powerful algorithms and artificial intelligence

Returns#

In order for an investment to be profitable, the money it yields must be higher than the inital investment made (plus transaction costs).

Assess so called return, usually discrete: relative change in investment value $S$.

\[ r_t = \frac{S_t - S_{t-1}}{S_{t-1}} =\frac{S_t}{S_{t-1}} - 1 \]

Note here that one time step $t$ is of arbitrary length, e.g. daily or monthly

Additivity#

Returns my be based on different time spans $\rightarrow$ aggreagte somehow

The property we are looking for is called addititvity: sum shorter-scale returns to get the larger-scale returns

Note that we can’t just split monthly returns into daily returns, this requires making assumptions on the distribution

Daily and weekly returns:
To calculate weekly returns from daily returns, we mustn’t use the daily return as is.

time $t$	0	1	2	3	4	5	6	7
prices $S_t$	100	110	121	110	132	105	112	105
return $r_t$	—	0.10	0.10	-0.09	0.2	-0.20	0.07	-0.06

If we simply added all returns, we’d find a weekly return of $r_{0,7} = 0.12$.
However, using the formula from above, we find that $$ r_{0,7} = \frac{S_7}{S_{0}} - 1 = \frac{105}{100} - 1 = 0.05 $$ and conclude that indeed daily returns cannot simply be added up in order to yield the weekly return.

We can calculate discrete returns simply by using a method of a Series object: .pct_change().
Note the NaN value for the first line.

df = pd.DataFrame({
    'S': [100, 110, 121, 110, 132, 105, 112, 105],
    },
index=list(range(8)))
df

	S
0	100
1	110
2	121
3	110
4	132
5	105
6	112
7	105

df['discrete_returns'] = df['S'].pct_change()
df

	S	discrete_returns
0	100	NaN
1	110	0.100000
2	121	0.100000
3	110	-0.090909
4	132	0.200000
5	105	-0.204545
6	112	0.066667
7	105	-0.062500

Portfolios and cross-sectional additivity#

A portfolio is a collection of investments, e.g. stocks. Portfolios are allocated differently, i.e., by a degree of risk. We can describe a portfolio’s value by the sum of the value of its constituents.

We define the value of a single position $i$ by multiplying the number of stocks $N_i$ with the stock value $S_i$

\[ P_i = N_i \cdot S_i \]

The Total portfolio value is the sum of all position values:

\[ P = \sum_i P_i = \sum_i N_i \cdot S_i \]

The weight of company $i$ in the portfolio is then

\[ w_i = \frac{P_i}{P} = \frac{N_i \cdot S_i}{\sum_j N_j \cdot S_j}, \sum_i w_i = 1 \]

With those weights, we can calculate the portfolio return (cross-sectional additivity) as weighted sum of the company returns $R_i$:

\[ R_p = \sum_i w_i \, R_i \]

We talk about a naive portfolio of $J$ stocks when all weights are equal $w = w_1 = w_2 = ... = w_J$. In this case, the weighted sum becomes the mean of all stock returns $R_i$, as $w = \frac{1}{J}$ and the portfolio return is

\[R_p = \frac{1}{J} \sum_i^JR_i = mean(R_i)\]

Portfolio return and cross-sectional additivity#

We can show that property using the definitons from above

Price evolution for single stock $i$:

\[ P_{t+1}^i = P_t^i \,(1 + r_{t+1}^i) \]
Plugging this into the Portfolio value:

\[ P_{t+1}^{PF} = \sum_i P_{t+1}^i = \sum_i P_t^i \,(1 + r_{t+1}^i)\]

With the “regular” formula for discrete returns, the Portfolio return is:

\[ r_{t+1}^{PF} = \frac{P_{t+1}^{PF}}{P_t^{PF}} - 1 = \frac{\sum_i P_t^i (1 + r_{t+1}^i)}{\sum_j P_t^j} - 1 = \sum_i \frac{P_t^i}{\sum_j P_t^j}(1 + r_{t+1}^i) - 1 = \sum_i w_i\,(1 + r_{t+1}^i) - 1 = \sum_i w_i\,r_{t+1}^i \]

Let’s have a look at the following data:

time $t$	0	1	2	3	4	5	6	7
company A $A_t$	100	110	121	110	132	105	112	105
company B $B_t$	100	120	124	118	117	135	128	115

For simplicity, we will assume to invest the same amount of money in both stocks. This gives initial portfolio weights $w_1=w_2=0.5$. For such a naive portfolio, we can then just apply the mean, i.e. the portfolio return on day $t$ is just the mean of all returns $r_{i,t}$ for all companies $i$.

Calculate the daily returns of the portfolio using pandas:

df = pd.DataFrame({
    'A': [100, 110, 121, 110, 132, 105, 112, 105],
    'B': [100, 120, 124, 118, 117, 135, 128, 115],
    },
index=list(range(8)))
df

	A	B
0	100	100
1	110	120
2	121	124
3	110	118
4	132	117
5	105	135
6	112	128
7	105	115

When we want to calculate the returns for a naive portfolio, we simply calculate the mean over all returns. This give us the daily (naive) portfolio returns over time.

df_prices_and_returns = df.copy()
df_prices_and_returns['A_return'] = df_prices_and_returns.A.pct_change()
df_prices_and_returns['B_return'] = df_prices_and_returns.B.pct_change()
# mean applied to axis=1, means we calculate the row mean (axis=0 will calculate the column mean)
df_prices_and_returns.loc[1:,'naive_pf_return'] = df_prices_and_returns.loc[1:,['A_return', 'B_return']].mean(axis=1)
df_prices_and_returns

	A	B	A_return	B_return	naive_pf_return
0	100	100	NaN	NaN	NaN
1	110	120	0.100000	0.200000	0.150000
2	121	124	0.100000	0.033333	0.066667
3	110	118	-0.090909	-0.048387	-0.069648
4	132	117	0.200000	-0.008475	0.095763
5	105	135	-0.204545	0.153846	-0.025350
6	112	128	0.066667	-0.051852	0.007407
7	105	115	-0.062500	-0.101562	-0.082031

We can apply .pct_change() to the whole dataframe, to create a new one with the same column names.

df_just_returns = df.copy()
df_just_returns = df_just_returns.pct_change()
df_just_returns

	A	B
0	NaN	NaN
1	0.100000	0.200000
2	0.100000	0.033333
3	-0.090909	-0.048387
4	0.200000	-0.008475
5	-0.204545	0.153846
6	0.066667	-0.051852
7	-0.062500	-0.101562

Characteristics of returns#

Usually, returns exhibit the following:

expected returns are close to zero (the shorter the time span, the smaller the expected return)
weakly stationary (i.e. constant expected value and variance over time) but usually volatility clustering
skewed distribution

From these items alone, we can start an analysis of stock returns by looking at some (standardized) moments of the empirical data:

the average return as an estimate of the expected return
the empirical variance or standard deviation/volatility

Use pandas, by calling the appropriate methods.

We will have a look at real-world data, downloading close prices using the yfinance package and calculating the returns.

data = pd.read_csv('./data/historical_data.csv', index_col=0)[['MSFT_Adj Close', 'BA_Adj Close']].reset_index()

data['daily_discrete_return_msft'] = data['MSFT_Adj Close'].pct_change()
data['daily_discrete_return_ba'] = data['BA_Adj Close'].pct_change()
data.dropna(inplace=True)
print(data['Date'].min(), data['Date'].max())
data = data[['Date', 'daily_discrete_return_msft', 'daily_discrete_return_ba']]
data.head(3)

2016-06-15 2021-06-11

	Date	daily_discrete_return_msft	daily_discrete_return_ba
1	2016-06-15	-0.002810	-0.002605
2	2016-06-16	0.014087	-0.006070
3	2016-06-17	-0.005160	0.003479

avg_return = data['daily_discrete_return_msft'].mean()
vola = data['daily_discrete_return_msft'].std()

print(f'MSFT: average return {np.round(avg_return,4)}')
print(f'MSFT: volatility {np.round(vola, 4)}')

MSFT: average return 0.0015
MSFT: volatility 0.0173

When investing in stocks, it is quite clear that we prefer a higher return to a lower (or even negative) return. However “There ain’t no such thing as a free lunch”, meaning that there is always a trade-off when looking for ever higher returns: the risk associated with these investments. We can also look this the other way round, namely that an investor would expect a higher return from investing in a more risky asset. A simple proxy used for risk in the stock market is how much a stock’s price moves up and down over time, since the classic framework weighs a loss in stock price heavier than an increase due to a non-linear utility function. Now, for historical data, we can measure this type of risk as the standard deviation. When taking the ratio of the historical average return over the standard deviation, we can calculate the so-called Sharpe ratio:

\[ SR = \frac{\bar{r_t}}{\sigma_t} .\]

When comparing two companies, we would choose the one with the higher Sharpe ratio, as it would yield (or rather has yielded) higher returns in relation to the associated risk.
Consider, for example, two companies $A$ and $B$ with returns $\bar{r_A}$ and $\bar{r_B}$, standard deviations $\sigma_A$ and $\sigma_B$, and sharpe ratios $SR_A > SR_B$:

If $\bar{r_A}$ = $\bar{r_B}$, it follows that $\sigma_A < \sigma_B$: while yielding the same return, company $A$ was less risky.
If $\sigma_A = \sigma_B$, it follows that $\bar{r_A} > \bar{r_B}$: while the risk of investing was the same for $A$ and $B$, company $A$ yielded higher returns.

We can caluclate the Sharpe ratios from return data:

sharpe_msft = data['daily_discrete_return_msft'].mean() / data['daily_discrete_return_ba'].std()
sharpe_ba = data['daily_discrete_return_ba'].mean() / data['daily_discrete_return_ba'].std()
print(f'Sharpe ratio {sharpe_msft.round(4)}')
print(f'Sharpe ratio {sharpe_ba.round(4)}')

Sharpe ratio 0.0524
Sharpe ratio 0.0345

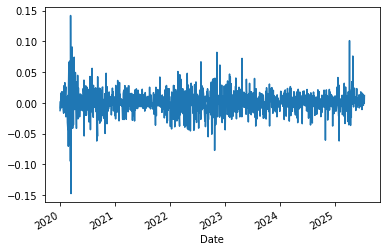
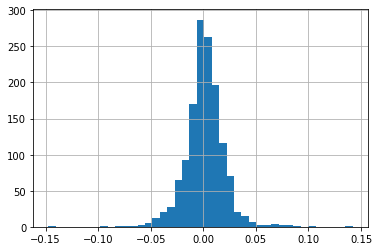
As we discussed in earlier chapter, it is always recommended to take a look at some charts.
We can plot returns over time as well as look at the distribution.

data['daily_discrete_return_msft'].plot(figsize=(5,4))

<AxesSubplot: >

_images/0f3f56ae8290d4dde1551b7607bf2daaf7b60e75cac2a9f7748a46ea03e5935b.png

data['daily_discrete_return_msft'].hist(bins=41, figsize=(5,4))

<AxesSubplot: >

_images/a700cfdb0cc7ff37fc89e23d87bbabb6cbd4fb482c5319510b97058e1274cb6b.png

The CAPM factor-model and excess returns#

The Captial Asset Pricing Model in its most simple form (Sharpe, Lintner) quantifies an assets risk with regard to non-diversifiable market risk.

Risk can usually be attributed to two sources: idiosyncratic and systematic (market) risk

Idiosyncratic risk can be eliminated by constructing a diversified portfolio, systematic risk remains

Use ordinary least squares (OLS) model to estimate:

\[ r_{i,t} - r_{f,t} = \alpha + \beta \cdot (r_{M,t} - r_{f,t}) + \epsilon_{i,t}\]

assume a risk-free rate of $r_{f,t}=0$:

\[ r_{i,t} = \alpha_i + \beta_i \cdot r_{M,t} + \epsilon_{i,t}\]

about the coefficients#

In general $\alpha_i$ should not be statistically significant for the model to be valid

Assuming it in fact isn’t, $\beta_i$ tells us about the sensitivity of the asset with regard to market risk:

for $\beta=1$ an asset’s expected return is assumed to match the expected market return
for $\beta >1$ an asset is more volatile than the market and thus considered more risky than the market
for $\beta <1$ an asset is less volatile than the market and considered less risky than the market

Note:

we can never know the market return which we use as a benchmark $\rightarrow$ use a proxy like the S&P 500

sp_500 = pd.read_csv('./data/SP500.csv')[-200:]
sp_500['Date'] = pd.to_datetime(sp_500['Date'])
sp_500 = sp_500[['Date', 'close']]
sp_500.head(1)

	Date	close
1077	2020-08-25	3443.620117

msft = data[['Date', 'daily_discrete_return_msft']][-200:].copy()
msft['Date'] = pd.to_datetime(msft['Date'])
msft.head(1)

	Date	daily_discrete_return_msft
1058	2020-08-26	0.02162

# excess returns by subtracting r_f
# if r_f is not constant, but changing over time, we would merge the r_f column to the discrete returns  
# to match the days, then subtract it from the returns to get excess returns
# assume
rf = 0.0

msft['daily_excess_return'] = msft['daily_discrete_return_msft'] - rf
sp_500['daily_excess_return'] = sp_500['close'].pct_change() - rf

sp_500.isnull().sum()

Date                   0
close                  0
daily_excess_return    1
dtype: int64

msft.dropna(inplace=True)
sp_500.dropna(inplace=True)

sp_500.columns = [el+'_sp' for el in sp_500.columns] 